1. Khối 10
  2. Bài tập và kiểm tra đánh giá Toán 10 - Tập một
  3. CHƯƠNG IV VECTƠ
  4. Chủ đề 2. Tổng và hiệu của hai vectơ
  5. Ví dụ
  • Ví dụ 111. (Nhận biết các quy tắc cộng và trừ hai vectơ)
    Cho bốn điểm A,B,C,DA, B, C, DA,B,C,D phân biệt. Khẳng định nào sau đây là SAI\mathrm{SAI}SAI? A. ABundefined+BCundefined+CDundefined=ADundefined\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}=\overrightarrow{A D}AB+BC+CD=AD. B. BAundefined−CAundefined+CBundefined=0undefined\overrightarrow{B A}-\overrightarrow{C A}+\overrightarrow{C B}=\overrightarrow{0}BA−CA+CB=0. C. BCundefined−ACundefined=BAundefined\overrightarrow{B C}-\overrightarrow{A C}=\overrightarrow{B A}BC−AC=BA. D. ABundefined−ACundefined=BCundefined\overrightarrow{A B}-\overrightarrow{A C}=\overrightarrow{B C}AB−AC=BC.
    Phân tích: Phương án A\mathrm{A}A xét tổng của ba vectơ ABundefined,BCundefined\overrightarrow{A B}, \overrightarrow{B C}AB,BC và CDundefined\overrightarrow{C D}CD nên ta sử dụng quy tắc ba điểm để kiểm tra tính đúng sai. Phương án B,C\mathrm{B}, \mathrm{C}B,C có phép toán hiệu của hai vectơ không chung gốc nên ta sử dụng phép biến đổi vectơ đối để đưa về sử dụng quy tắc ba điểm. Phương án D\mathrm{D}D ta sử dụng trực tiếp quy tắc trừ để kiểm tra.
    Hướng dẫn giải: Ta có ABundefined+BCundefined+CDundefined=(ABundefined+BCundefined)+CDundefined=ACundefined+CDundefined=ADundefined\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}=(\overrightarrow{A B}+\overrightarrow{B C})+\overrightarrow{C D}=\overrightarrow{A C}+\overrightarrow{C D}=\overrightarrow{A D}AB+BC+CD=(AB+BC)+CD=AC+CD=AD. Phương án A\mathrm{A}A là đúng. Ta có BAundefined−CAundefined+CBundefined=BAundefined+ACundefined+CBundefined=BCundefined−BCundefined=0undefined\overrightarrow{B A}-\overrightarrow{C A}+\overrightarrow{C B}=\overrightarrow{B A}+\overrightarrow{A C}+\overrightarrow{C B}=\overrightarrow{B C}-\overrightarrow{B C}=\overrightarrow{0}BA−CA+CB=BA+AC+CB=BC−BC=0. Phương án B\mathrm{B}B là đúng. Ta có BCundefined−ACundefined=BCundefined+CAundefined=BAundefined\overrightarrow{B C}-\overrightarrow{A C}=\overrightarrow{B C}+\overrightarrow{C A}=\overrightarrow{B A}BC−AC=BC+CA=BA. Phương án CCC là đúng. Áp dụng quy tắc hiệu của hai vectơ, ta có ABundefined−ACundefined=CBundefined\overrightarrow{A B}-\overrightarrow{A C}=\overrightarrow{C B}AB−AC=CB. Phương án D\mathrm{D}D là sai. Đáp án là D\mathrm{D}D.
    Đáp án
    1/1
  • Ví dụ 222. (Biểu thị một số đại lượng trong thực tiễn bằng vectơ)
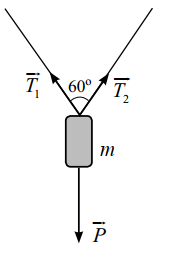
    Một vật có khối lượng mmm được treo cố định trên trần nhà bằng hai sợi dây không dãn có độ dài như nhau. Biết rằng lực căng dây Tundefined1\overrightarrow{T}_{\tiny 1}T1​ và Tundefined2\overrightarrow{T}_{\tiny 2}T2​ có độ lớn như nhau bằng 600 N600 \mathrm{~N}600 N và hợp với nhau một góc 60∘60^{\tiny \circ}60∘ (hình bên). Trọng lượng của vật là A. 600 N600 \mathrm{~N}600 N. B. 6003 N600 \sqrt{3} \mathrm{~N}6003​ N. C. 1 200 N1~200 \mathrm{~N}1 200 N. D. 1 2003 N1~200 \sqrt{3} \mathrm{~N}1 2003​ N.
    Phân tích: Trọng lực Pundefined\overrightarrow{P}P của vật có cùng độ lớn và ngược chiều với hợp lực Tundefined12\overrightarrow{T}_{\tiny 12}T12​ là tổng của hai lực Tundefined1\overrightarrow{T}_{\tiny 1}T1​ và Tundefined2\overrightarrow{T}_{\tiny 2}T2​. Mặt khác, ta có góc giữa hai lực Tundefined1\overrightarrow{T}_{\tiny 1}T1​ và Tundefined12\overrightarrow{T}_{\tiny 12}T12​ bằng 30∘30^{\tiny \circ}30∘. Do đó ta tính độ lớn của lực T12undefined\overrightarrow{T_{\tiny 12}}T12​​ thông qua tỉ số lượng giác của góc 30∘30^{\tiny \circ}30∘.
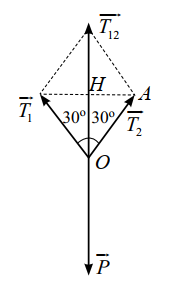
    Hướng dẫn giải: Hướng dẫn giải: Xét tam giác OAHO A HOAH như hình vẽ. Ta có ∣Tundefined12∣=2⋅OH=2⋅OA⋅cos⁡30∘=2⋅∣Tundefined2∣⋅cos⁡30∘\left|\overrightarrow{T}_{\tiny 12}\right|=2 \cdot O H=2 \cdot O A \cdot \cos 30^{\tiny \circ}=2 \cdot\left|\overrightarrow{T}_{\tiny 2}\right| \cdot \cos 30^{\tiny \circ}∣∣​T12​∣∣​=2⋅OH=2⋅OA⋅cos30∘=2⋅∣∣​T2​∣∣​⋅cos30∘ =2⋅600⋅32=6003 (N)=2 \cdot 600 \cdot \dfrac{\sqrt{3}}{2}=600 \sqrt{3}~(\mathrm{N})=2⋅600⋅23​​=6003​ (N). Vậy trọng lượng của vật là 6003 N600 \sqrt{3} \mathrm{~N}6003​ N. Đáp án là B\mathrm{B}B.
    Đáp án
    1/1

hoclieuthongminh.com © 2022

  • Sitemap
  • Home
  • Home