1. Khối 7
  2. Toán 7 - Cơ bản và nâng cao - Tập một
  3. Chương I Góc và đường thẳng song song
  4. §1. Góc ở vị trí đặc biệt
  5. Mức độ cơ bản
  • Ví dụ 222. Hai đường thẳng ABA BAB và CDC DCD cắt nhau tại OOO. Trên hình vẽ có mấy cặp góc kề bù?

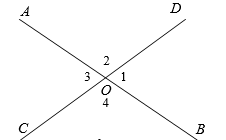
    hình 17

    Bài giải
    (h.17)(h. 17)(h.17) Có bốn cặp góc kề bù là O1undefined\widehat{O_{\tiny 1}}O1​​ và O2undefined,O1undefined\widehat{O_{\tiny 2}} , \widehat{O_{\tiny 1}}O2​​,O1​​ và O4undefined\widehat{O_{\tiny 4}}O4​​, O2undefined\widehat{O_{\tiny 2}}O2​​ và O3undefined,O3undefined\widehat{O_{\tiny 3}} , \widehat{O_{\tiny 3}}O3​​,O3​​ và O4undefined\widehat{O_{\tiny 4}}O4​​.
    Đáp án
    1/1
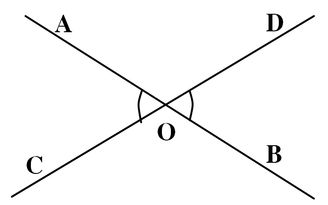
  • Ví dụ 1 11. Cho hai đường thẳng ABA BAB và CDC DCD cắt nhau tại OOO. Biết AODundefined−BODundefined=40∘\widehat{A O D}-\widehat{B O D}=40^{\tiny \circ}AOD−BOD=40∘. Tính các góc AOD,BOD,BOC,AOCA O D, B O D, B O C, A O CAOD,BOD,BOC,AOC.

    hình 16

    Bài giải
    (h.16) (h.16)(h.16) Ta có AODundefined+BODundefined=180∘\widehat{A O D}+\widehat{B O D}=180^{\tiny \circ}AOD+BOD=180∘ và AODundefined−BODundefined=40∘ neˆn \widehat{A O D}-\widehat{B O D}=40^{\tiny \circ} \text { nên }AOD−BOD=40∘ neˆn  AODundefined=(180∘+40∘):2=110∘,\widehat{A O D}=\left(180^{\tiny \circ}+40^{\tiny \circ}\right): 2=110^{\tiny \circ}, AOD=(180∘+40∘):2=110∘, BODundefined=110∘−40∘=70∘.\widehat{B O D}=110^{\tiny \circ}-40^{\tiny \circ}=70^{\tiny \circ} . BOD=110∘−40∘=70∘. Hai góc đối đỉnh thì bằng nhau nên BOCundefined=AODundefined=110∘,AOCundefined=BODundefined=70∘\widehat{B O C}=\widehat{A O D}=110^{\tiny \circ}, \widehat{A O C}=\widehat{B O D}=70^{\tiny \circ}BOC=AOD=110∘,AOC=BOD=70∘.
    Đáp án
    1/1

hoclieuthongminh.com © 2022

  • Sitemap
  • Home
  • Home