Toán bồi dưỡng học sinh lớp 4 | A. CÁC BÀI TOÁN | I. MỘT SỐ BÀI TOÁN VỀ SỐ TỰ NHIÊN VÀ PHÉP TÍNH VỚI SỐ TỰ NHIÊN Bài 41 | Học liệu thông minh

Tìm các số tự nhiên có $3$ chữ số biết rằng nếu xóa đi $2$ chữ số cuối của nó ta được $1$ số bằng $\dfrac{1}{125}$ số đã cho.
Trả lời:
Các số cần tìm là ; ; .
Đáp án
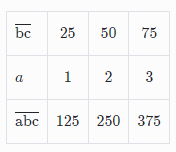
Các số cần tìm là $125$ ; $250$ ; $375$ .
Giải thích
Gọi số đó là $\overline{\mathrm{abc}}~(\mathrm{a} \neq 0)$ $\overline{\mathrm{abc}}=\mathrm{a} \times 125$ $\underbrace{\mathrm{a} \times 100 + \overline{\mathrm{bc}}}_{\mathrm{I}} = \underbrace{\mathrm{a} \times 100 +\mathrm{a} \times 25}_{\mathrm{II}}$ (nhân $1$ số với $1$ tổng) Vì $\mathrm{I}=\mathrm{II}$ , bớt cả hai biểu thức đi $\mathrm{a} \times 100$ , ta có $\overline{\mathrm{bc}}= \mathrm{a} \times 25$ Vậy $\overline{\mathrm{bc}}$ chia hết cho $25$ . $\overline{\mathrm{bc}}=25 ; 50 ; 75$
Vậy số đó là $125 ; 250 ; 375$ .

1/1